Mathématiques, Bac G Amérique du Sud 2025.

Exercice 1 6 points
Dans cet exercice, tous les résultats seront arrondis à 10⁻³ près en cas de besoin. Les deux parties de cet exercice sont indépendantes l’une de l’autre. +
Partie A
Au tennis, le joueur qui est au service peut, en cas d’échec lors du premier service, servir une deuxième balle. En match, Abel réussit son premier service dans 70 % des cas. Lorsque le premier service est réussi, il gagne le point dans 80 % des cas. En revanche, après un échec à son premier service, Abel gagne le point dans 45 % des cas. Abel est au service. On considère les évènements suivants :
S : « Abel réussit son premier service »; G : « Abel gagne le point ».
1. Décrire l’évènement non S puis traduire la situation par un arbre pondéré.
Evénement non S : Abel ne réussit pas son premier service.
2. Calculer P(S ∩G).
3. Justifier que la probabilité de l’évènement G est égale à 0,695.

4. Abel a gagné le point. Quelle est la probabilité qu’il ait réussi son premier service?
0,56 / 0,695 ~0,806.
5. Les évènements S et G sont-ils indépendants? Justifier.
P(S n G) = 0,56.
P(S) x P(G) = 0,7 x0,695=0,4865, diffère de 0,56.
Les événement S et G ne sont pas indépendants.
Partie B
À la sortie d’une usine de fabrication de balles de tennis, une balle est jugée conforme dans 85% des cas.
1. On teste successivement 20 balles. On considère que le nombre de balles est suffisamment grand pour assimiler ces tests à un tirage avec remise. On note X la variable aléatoire qui compte le nombre de balles conformes parmi les 20 testées.
a. Quelle est la loi suivie par X et quels sont ses paramètres? Justifier.
Cette épreuve élémentaire 20 fois ; le nombre de balles est suffisamment grand pour assimiler ces tests à un tirage avec remise.
La variable aléatoire X qui compte le nombre de balles conformes parmi les 20 testées, suit la loi binomiale de paramètres n = 20 et p = 0,85.
b. Calculer P(X < 18).
La calculatrice donne : P(X < 18)~0,824.
c. Quelle est la probabilité qu’au moins deux balles ne soient pas conformes parmi les 20 balles testées ?
La probabilité qu’au moins deux balles ne soient pas conformes parmi les 20 balles testées est égale à la probabilité qu’au plus 18 balles soient conformes, soit P (X < 18) ~ 0,824
d. Déterminer l’espérance de X.
E(X) = n p = 20 x0,85=17.
2. On teste maintenant n balles successivement. On considère les n tests comme un échantillon de n variables aléatoires X indépendantes suivant la loi de Bernoulli de paramètre 0,85.
On considère la variable aléatoire

a. Déterminer l’espérance et la variance de M_n.
Les n variables aléatoires X indépendantes suivent la loi de bernoulli de paramètre p = 0,85.
Espérance p = 0,85 ; variance : p(1-p) =0,85 x0,25 = 0,1275.
S_n = X₁ +X₂ +...+X_n.
D'après la linéarité de l'espérance : E(S_n) = 0,85 n.
Les variables X_iétant indépendantes, l'additivité de la variance donne :
V(S_n) = 0,1275 n.
b. Après avoir rappelé l’inégalité de Bienaymé-Tchebychev, montrer que, pour tout entier naturel n,
P(0,75 <M_n < 0,95)>1−12,75 /n.
Soit la variable aléatoire X et t un réel positif, l’inégalité de Bienaymé-Tchebychev s'écrit :
P(|X-E(X)|< t) < V(X) / t².
P(|X-E(X)|< t) >1-V(X) / t².
P(|M_n-E(M_n)| < t) > 1-V(X) / t².
P(|M_n-0,85| < t) > 1-0,1275 / (nt²).
Pour t = 0,1 :
|M_n-0,85| < t équivalent à |M_n-0,85| < 0,1 équivalent à : -0,1 < M_n -0,85 <0,1.
0,75 < M_n < 0,95.
1-0,1275 / (nt²)= 1-0,1275 / (0,01 n)=1-12,75 / n.
P(0,75 <M_n < 0,95)>1−12,75 /n.
c. En déduire un entier n tel que la moyenne du nombre de balles conformes pour un échantillon de taille n appartienne à l’intervalle ]0,75; 0,95 [ avec une probabilité supérieure à 0,9.
Il suffit que 1-12,75 / n > 0,9.
0,1 > 12,75 / n.
0,1 n > 12,75 ; n > 127,5.
Taille de l'échantillon n = 128.

Exercice 2 . QCM. 4 points.
Cet exercice est un questionnaire à choix multiple. Pour chaque question, une seule des trois propositions est exacte.
Indiquer sur la copie le numéro de la question et la lettre de la proposition choisie.
Aucune justification n’est demandée.
Pour chaque question, une réponse exacte rapporte un point.
Une réponse fausse, une réponse multiple ou l’absence de réponse ne rapporte ni n’enlève de point.
Dans toutes les questions suivantes, l’espace est rapporté à un repère orthonormé.
1. On considère la droite D₁ de représentation paramétrique :
x = 1−3t
y = 4+2t
z = t , où t est un réel.
ainsi que la droite D₂ de représentation paramétrique :
x = −4+ s
y = 2+2s
z = −1+ s , où sest un réel.
a. Les droites D₁ et D₂ sont parallèles. Faux.
b. Les droites D₁ et D₂ sont orthogonales. Faux.
c. Les droites D₁ et D₂ sont sécantes. Vrai.
Coordonnées des vecteurs directeurs des droites :
D₁ : -3 ; 2 ; 1.
D₂ : 1 ; 2 ; 1.
Ces vecteurs n'étant pas colinéaires, les droites ne sont pas parallèles.
En remplaçant t par 1 et s par 2, on trouve le point de coordonnées (-2 ; 6 ; 1) qui appartient aux deux droites.

2. On considère la droite d de représentation paramétrique :
x = 1+ t
y = 3− t
z = 1+2t , où t est un réel
et le plan P d’équation cartésienne : 4x +2y −z +3 =0.
a. La droite d est incluse dans le plan P. Faux.
b. La droite d est parallèle strictement au plan P. Vrai.
c. La droite d est sécante au plan P.Faux.
Le point M de coordonnées x_M = 1+t , y_M=3-t, z_M = 1+2t appartient au plan P si 4x_M +2y_M −z_M +3 =0.
4(1+t)+2(3-t)-1-2t+3=0.
4+4t+6-2t-1-2t+3=0
12+0t=0.
Cette équation n'ayant pas de solution, la droite d est strictement parallèle au plan P.

3. On considère les points A(3; 2; 1), B(7; 3 ; 1), C(−1 ; 4 ; 5) et D(−3 ; 3 ; 5).
a. Les points A, B, C et D ne sont pas coplanaires. Vrai.
b. Les points A, B et C sont alignés. Faux.
c. Les vecteurs AB et CD sont colinéaires. Faux.

Hypothèse : A, B, C et D sont coplanaires, alors :

Cette égalité vectorielle se traduit par le système suivant :
-6=4x-4y ; 1=x+2y ; 4 = 4y.
y =1 ;
-6=4x-4 ; x= -0,5.
x+2y=-0,5+2=1,5 diffère de 1.
Le système n'ayant pas de solution, D n'appartient pas au plan défini par les points A, B et C.
Les points A, B, C et D ne sont pas coplanaires..

4. On considère les plans Q et Q′ d’équation cartésienne respective 3x −2y +z +1 = 0 et
4x + y −z +3 =0.
a. Le point R(1 ; 1 ; −2) appartient aux deux plans. Faux.
b. Les deux plans sont orthogonaux. Faux.
c. Les deux plans sont sécants avec pour intersection la droite de représentation paramétrique
x = t
y = 7t +4
z = 11t +7 avec t réel. Vrai.

3x_R −2y_R +z_R +1 =3-2-2+1=0. R appartient au plan Q.
4x_R +y_R -z_R +3 =4+1+2+3 diffère de zéro : . R n'appartient pas au plan Q'.

Coordonnées d'un vecteur orthogonal au plan Q : 3 ; -2 ; 1.
Coordonnées d'un vecteur orthogonal au plan Q' : 4 ; 1 ; -1.
Le produit scalaire de ces deux vecteurs 3*4-2*1-1*1 =9 diffère de zéro. Ces vecteurs ne sont pas orthogonaux.

Les coordonnées des points communs aux deux plans vérifient le système 3x −2y +z +1 = 0 et 4x + y −z +3 =0.
On pose x = t, avec t réel.
3t+4t-2y+y+z-z+1+3=0
7t-y+4=0 ; y = 7t+4.
3t-2(7t+4)+z+1=0 ; -11t+z-7=0 ; z = 11t+7.
3t-2(7t+4)+11t+7+1=0 ; 0t -8+8 =0 est vérifié.
4t+7t+4-11t-7+3= 0t+0=0 est bien vérifié.
Coordonnées des points communs aux deux planx : x=t ; y =7t+4 ; z = 11t+7 avec t réel.

Exercice 3 4 points
On considère les suites (v_n) et (w_n) définies pour tout entier naturel n par :
v₀ = ln(4)
v_n+1 = ln(−1+2exp(v_n) )
et w_n =−1+exp(v_n) .
On admet que la suite (v_n) est bien définie et strictement positive.
1. Donner les valeurs exactes de v₁ et w₀.
v₁ = ln(-1+2 exp(ln(4))) = ln(-1+8) = ln(7).
w₀=-1+exp(v₀) = -1 +exp(ln(4)) = -1+4=3.
2. a. Une partie d’une feuille de calcul où figurent les indices et les termes des suites (v_n) et (w_n) est reproduite ci-dessous.

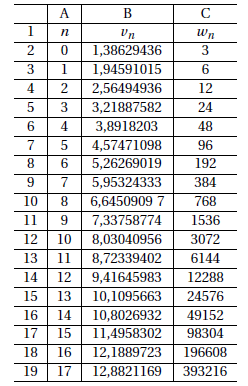
Parmi les trois formules ci-dessous, choisir la formule qui, saisie dans la cellule B3 puis recopiée vers le bas, permettra d’obtenir les
valeurs de la suite (v_n) dans la colonne B.
Formule 1: LN(−1+2 * EXP(B2))
Formule 2 : = LN(−1+2 * EXP(B2))
Formule 3 : = LN(−1+2 * EXP(A2))
b. Conjecturer le sens de variation de la suite (v_n).
La suite (v_n) est croissante.
c. À l’aide d’un raisonnement par récurrence, valider votre conjecture concernant le sens de variation de la suite (v_n).
Initialisation : v₁ = ln(7) ; v₀ = ln(4) ; la propriété est vraie au rang 0.
Hérédité : v_n+1 > v_n est supposé vrai.
exp(v_n) < exp(v_n+1) par croissance de la fonction exponentielle.
2 exp(v_n) < 2 exp(v_n+1)
-1+2 exp(v_n) < -1+2 exp(v_n+1).
ln(-1+2 exp(v_n) )<ln(-1+2 exp(v_n+1)) par croissance de la fonction logarithme népérien..
v_n+2 > v_n+1.
Conclusion : La propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier naturel n.
3. a. Démontrer que la suite (w_n) est géométrique.
w_n+1 =−1+exp(v_n+1) et v_n+1 = ln(−1+2exp(v_n) ).
w_n+1 =−1+exp(ln(−1+2exp(v_n) )).
w_n+1 =−1+(-1+2exp(v_n)) =-2+2exp(v_n)) = 2(-1+exp(v_n)))=2 w_n.
La suite (w_n) est géométrique de raison 2 et de premier terme w₀ =3.
b. En déduire que pour tout entier naturel n, v_n = ln(1+3×2ⁿ ).
w_n= 3 x2ⁿ=−1+exp(v_n).
1+3×2ⁿ =exp(v_n) ; v_n = ln(1+3×2ⁿ ).
c. Déterminer la limite de la suite (v_n).
En plus l'infini : 2ⁿ tend vers +oo.
1+3x2ⁿ tend vers +oo ; ln(1+3×2ⁿ ) tend vers +oo.
.
4. Justifier que l’algorithme suivant écrit en langage Python renvoie un résultat quel que soit le choix de la valeur du nombre S.

Cet algorithme permet le calcul des termes de la suite (v_n) à partir de v₀.
On vient de démontere que cette suite n'est pas majorée.
Quel que soit le nombre S, il existe un rang p tel que vp > S ; l'algorithme donnera ce rang.

Exercice4. 6 points
Partie A : dénombrement
On considère l’ensemble des nombres entiers relatifs non nuls compris entre −30 et 30; cet ensemble peut s’écrire ainsi : {−30 ; −29 ; −28 ; ...−1 ; 1 ; ... ; 28 ; 29 ; 30}. Il comporte 60 éléments.
On choisit dans cet ensemble successivement et sans remise un entier relatif a puis un entier relatif c.
1. Combien de couples (a ; c) différents peut-on ainsi obtenir ?
Le premier terme a peut être choisi parmi 60 entiers.
Il n'y a pas de remise,et le couple (a ; c) diffère du couple ( c ; a) le second terme c peut être choisi parmi 59 entiers.
On peut obtenir 60 x59 =2540 couples différents.
On considère l’évènement M : « l’équation ax² +2x +c = 0 possède deux solutions réelles distinctes », où a et c sont les entiers relatifs précédemment choisis.
2. Montrer que l’évènement M a lieu si et seulement si ac < 1.
Discriminant : 2²-4ac =4(1-ac)> 0.
ac < 1.
3. Expliquer pourquoi l’évènement contraire non M comporte 1 740 issues.
L'évnement contraire est ac > 1.
Les couples (1 ; 1) et (-1 ; -1) sont impossibles ; donc ac > 1.
Si le premier terme est négatif ( 30 possibilités), le second sera négatif ( 29 posibilités) : 30 x29 = 870 couples.
De même si les deux termes sont positifs : 870 couples.
Total 1740 couples.
4. Quelle est la probabilité de l’évènement M. On arrondira le résultat à 10⁻².
L'événement M sera réalisé pour 3540-1740=1800 couples.
p5M) = 1800 / 3540 =30 /59 ~0,508.

Partie B : équation différentielle
On considère l’équation différentielle
(E) : y′+10y =(30x² +22x −8)e^−5x+1 avec x réel
où y est une fonction définie et dérivable sur R.
1. Résoudre sur R l’équation différentielle : y′ +10y =0.
f(x) = A exp(-10x) avec A une constante réelle.
2. Soit la fonction f définie sur R par
f (x) = (6x² +2x −2)e^−5x+1.
On admet que f est dérivable sur R et on note f ′ la fonction dérivée de la fonction f .
Justifier que f est une solution particulière de (E).
Calcul de f '(x) en posant u = 6x²+2x-2 et v = exp(-5x+1) ;
u' = 12x+2 ; v'= -5 exp(-5x+1).
u'v+v'u = (12x+2) exp(-5x+1) -5(6x²+2x-2) exp(-5x+1) =(-30x²+2x+12)exp(-5x+1).
Repport dans (E) :
(-30x²+2x+12)exp(-5x+1)+ 10(6x² +2x −2)exp(-5x+1) =(30x²+22x-8)exp(-2x+1).
3. Donner l’expression de toutes les solutions de (E).
Somme de f et des solutions de l'équation y'+10y=0, soit :
(6x² +2x −2)exp(-5x+1) + A exp(-10x).

Partie C : étude de fonction
On propose d’étudier dans cette partie la fonction f rencontrée à la partie B question 2.
On rappelle que, pour tout réel x , f (x) =(6x² +2x −2)e^−5x+1.
On note f ′ la fonction dérivée de la fonction f . On appelle Cf la courbe représentative de f dans un repère du plan.
1. On admet que la limite de f en plus l'infini est nulle.
Déterminer la limite de la fonction f en moins l'infini.
6x²+2x+2 tend vers +oo ; exp(-5x+2) tend vers +oo.
Par produit des limites, f(x) tend vers +oo.
2. En utilisant la partie A, montrer que Cf coupe l’axe des abscisses en deux points (les coordonnées de ces points ne sont pas attendues).
exp(-5x+1) >0, le signe de f(x) est celui du trinôme 6x²+2x-2.
a = 6 et c = -2 ; ac < 1 : le trinôme vérifie l'événement M.
Le trinome s'annule pour deux réel distincts : géométriquement la courbe Cf coupe l'axe des abscisses en deux points.
Discriminant :2²+4*2*6=52 = 4 *13.
Racines x₁ = (2 +52^½) / 12 =(1+13^½) / 6 ~0,77.
x₁ = (2 -52^½) / 12 =(1-13^½) / 6 ~ -0,43.
3. En utilisant les parties A et B, montrer que Cf possède deux tangentes horizontales.
f '(x)=(-30x²+2x+12)exp(-5x+1).
exp(-5x+1) > 0 ;
f '(x) s'annule pour -30x²+2x+12=0.
Discriminant : 2²+ 4*12*30=1444 =38².
x₁ =(-2+38) / (-60)=-36/60= -3 /5 ; x₂ =(-2-38) / (-60)=40/60= 2 /3.
Aux points d'abscisses -3 /5 et 2 /3, le nombre dérivé est nul : la tangente à la courbe Cf en ces deux points est horizontale.
f(-3 /5) ~ -56,8 ; f(2 /3) ~0,19.
4. Dresser le tableau de variation complet de la fonction f .

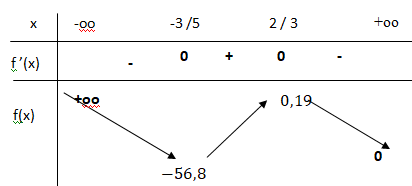5. Déterminer en justifiant le nombre de solution(s) de l’équation f (x) = 1.
Sur ]-oo ; -3/5[, f(x) décroît de plus l'infini à -56,8 :d'après le théorème des valeurs intermédiaires, il existe un réel a de cet intervalle tel que f(a) = 1.
Sur ]-3/5 ; +oo[, f(x) < 0,19< 1 :sur cet intervalle f(x) =1 n'a pas de solution.
6. Pour tout réel m strictement supérieur à 0,2, on définit I_m par :

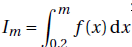a. Vérifier que la fonction F définie sur R par
F(x) =(-6x²/ 5-22x / 25+28 / 125) e^-5x+1
est une primitive de la fonction f sur R.
On calcule F '(x) en posant u = -6x²/5 -22 x / 25 +28 / 125 et v = exp(-5x+1).
u'=-12x/5 -22/25 ; v' = -5 exp(-5x+1).
u'v+v'u = (-12x / 5 -22 / 25 +6x²+22x /5-28 /25) exp(-5x+1)
F'(x) = (6 x²+2x -2)exp(-5x+1)=f(x).
b. Existe-t-il une valeur de m pour laquelle I_m = 0 ?
Interpréter graphiquement ce résultat.
I_m = F(m)-F(0,2).
F(0,2) =( -6 *0,2² / 5 -22*0,2 / 25 +28 /125) exp(0) =-0,048-0,176 +0,224= 0.
I_m = F(m)=(-6m²/ 5-22m / 25+28 / 125) e^-5m+1=0
L'exponentielle n'étant pas nulle, (-6m²/ 5-22m / 25+28 / 125 =0.
-150m² -110 m+28=0.
-75m²-55m+14=0.
Discriminant : 55²+4*14*75=7225 =85².
m₁ = (55+85)/(-150)= -140 / 150 = -14 /15 ; m₂= (55-85)/(-150)= 0,2.
-14/15 est négative, donc inférieure à 0,2.
Il n'existe pas de valeur de m pour laquelle I_m = 0.

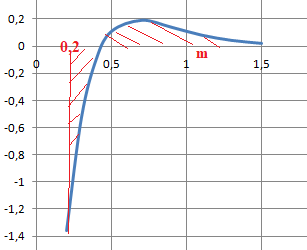
La surface hachurée limitée par le graphe de f, l'axe des abscisses et les droites d'équations x = 0,2 et x =m est égale à I_m.
Il n'existe pas de valeur de m telle que I_m =0 signifie que quelque soit m > 0,2, l'aire de la surface située au dessus de l'axe des abscisses n'est pas égale à l'aire de la surface située sous l'axe des abscisses.